How does the kicktail angle affect the pop?
Have you ever wanted to change your deck when a trick doesn't work?
For example, in a kickflip, you may feel that your front foot bites into your board more ithe tail is steeper, or you may feel that youcan pop more lightly if the tail is mellower. This time, we will analyze the true physics behind the kick tail angle.
Summary
Mellow tail angle requires less energy to pop
According to the physics simulator, a deck with the mellow tail angle popped high enough to flip with the small amount of energy. With the same energy, a deck with the steep tail angle did not even pop up into the air.
Mellow tail angle pops the highest
With a stronger pop, the mellow deck popped the highest compared to decks with steeper tails. This indicates although the mellow tail could transfer its energy to the ground immediately, the steep tail deck lost some of its potential energy while traveling for a longer distance before reaching the ground.
Important note
The result of this experiment focuses only on the effect of popping the tail. While a deck with the steepest kick tail angle did not pop the highest unlike the common saying, it does not directly translate it doesn't help you perform your tricks higher. Considering the nose of steep tail angle rises the highest when popped, it would help you lift it higher in an actual trick.
Making a real-life adjustable deck
Issues with the traditional skatebaord decks
Since this channel analyzes the science of skateboarding, I have always wanted to compare various tail angles, but I don't have much money to buy so many boards.
So, in this article, we will examine how the tail angle affects the performance of the board using multiple methods.
You can verify the tail angle of your choice using the pop simulator I will introduce later.

Introduction of used materials
First, I decided to make a board that I can freely adjust the tail angle. A blank deck and metal figgings were used. The fittings can be folded in the center, and I can fix their angles by tightening its central part.

Installing the fittings onto the deck
Next, holes were made to fix the metal fittings. After installing the hardware and the grip tape, it's complete. I can now change the tail's angle freely and fix it anywhere I want. Without having to buy a new deck, I should be able to experiment with different tail angles endlessly.

Result of the experiment
Lessons learned, at least
Sorry, it didn't work. The metal fixture was too weak, and I just couldn't make it strong enough to be used in an actual skateboarding scene.

Making a digital pop simulator
It's still too early to give up
What would be science without failure? If it's hard to create one in the real world, I can use a physics engine.
So, I made a simplified 3D model of a skateboard and coded the program, and the system's ready.
A Javascript library called Three.js and a physics library called cannon-es were used.

What can the system do?
This system allows you to adjust various elements of your choice, including the angle of the tail and nose.
For example, set the tail angle bigger and press the ReRun button, and the system will generate the tail with the specified angle and drop a sphere on top of it.

How to simulate a pop on this system
The generated sphere pushes down on the tail to simulate a pop.
Since the position of the end of the tail changes depending on the angle, the position at which the ball falls can also be adjusted.
Use the Auto Aim Tail function to automatically drop the sphere at the edge of the tail, as it takes some time to adjust it manually.

How to check the simulation result in slow motion
Furthermore, I have made it possible to adjust the flow of time in the 3D world for more detailed analysis so you can check the simulation in slow motion.
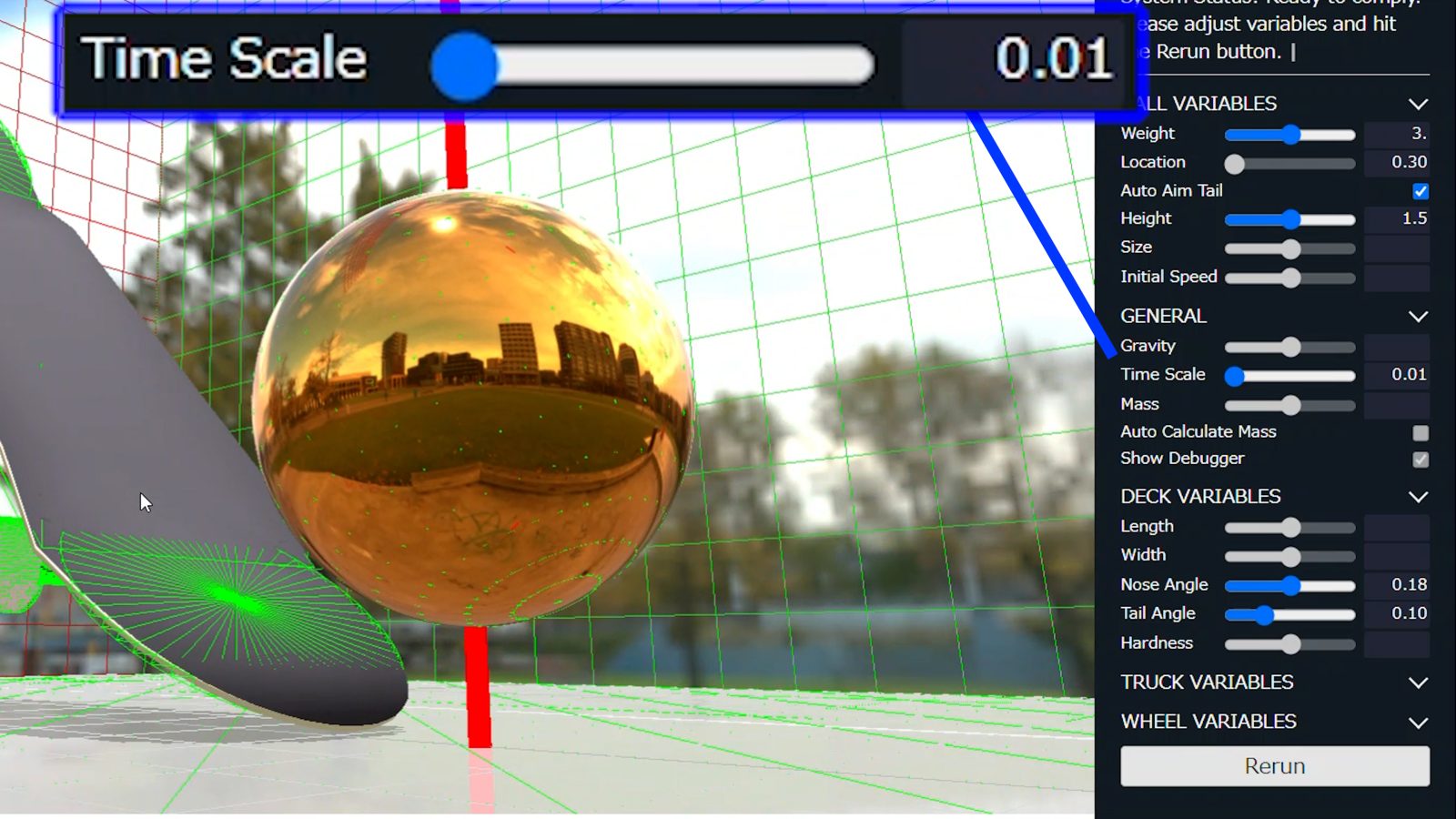
Important note on the system
Please note that some variables, such as the length and width of the board, cannot be controlled for now, as it's still under development.

Test conditions
Now, let's try this system under several conditions. It is generally said that "steeper the tail angle, the higher it pops"
span> or "mellower the tail angle, the lighter it pops." In order to verify whether these common beliefs are true, we will conduct a comparison test using boards with a 10-degree tail angle, an 18-degree tail angle, and a 36-degree tail angle.
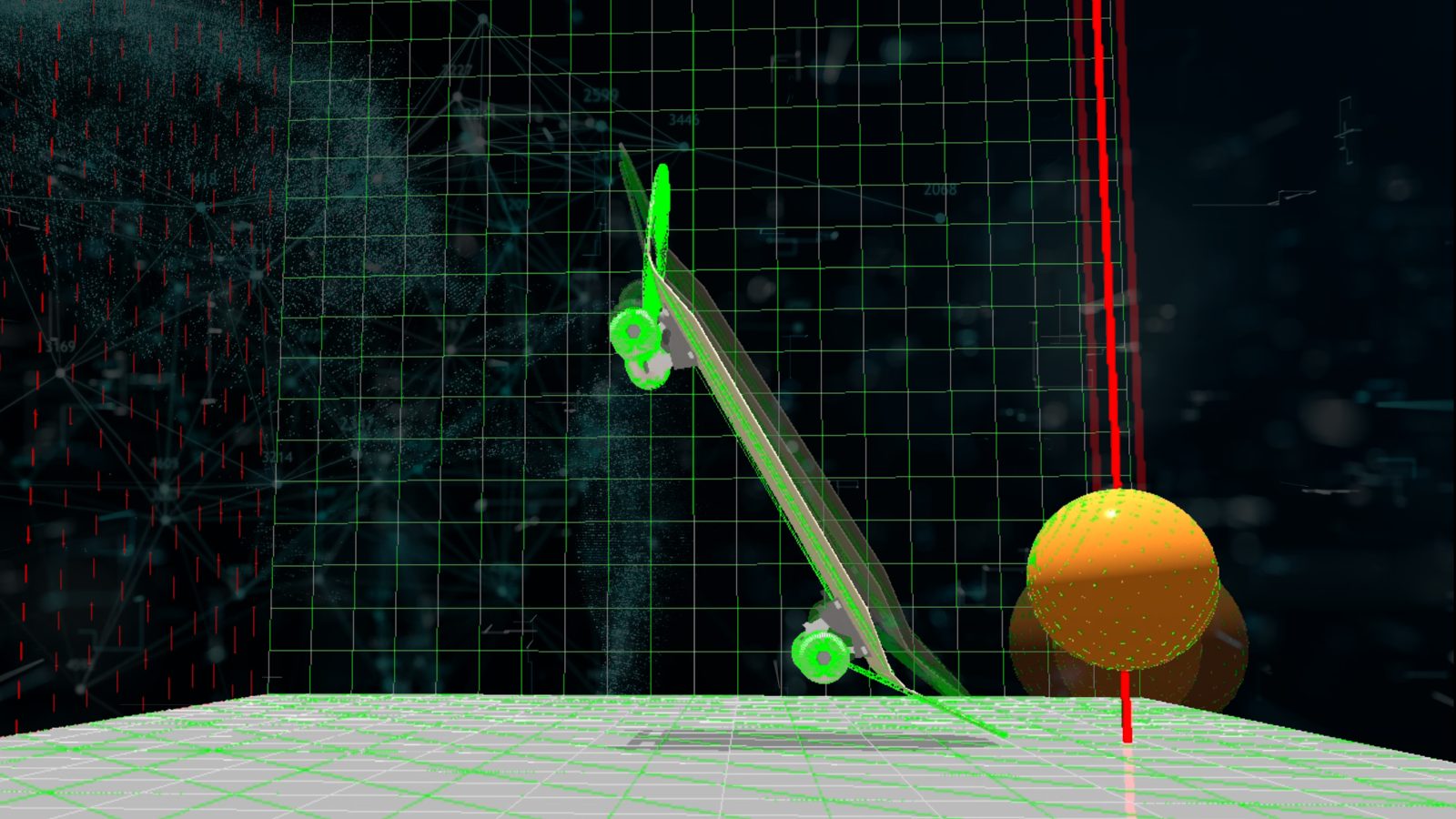
Simulation: Dropping a 3kg sphere from 1.5m high
The greater angle, the less it pops?
There was almost no difference between the 10-degree and 18-degree boards, and they flipped over to the other side.
However, the 36-degree board did not flip over to the other side and went back to its original direction.
This may be because the closer the tail is to vertical, the more force transfers to the ground rather than to lift the nose.

Note and the difference between the reality
Of course, not everything in this experiment applies to the real world; please keep in mind that the pop in the real world may contain a horizontal force and may change the way the board behaves.
Plus, the ease of doing tricks is an entirely different story. When I pop the board, you can see that the nose of the 36-degree board comes up significantly higher. This should make it easier to hook the front foot and lift the board more efficiently in an Ollie, and it should also make it easier to do flips.
Simulation: Dropping a 1.5kg sphere from 1.5m high
The 36-degree board pops the lowest
By simply comparing them, the angle of the 36-degree board seems to rise the highest, but there seems to be a hidden secret here.
Let's take a closer look: the 36-degree board starts to rise the moment the sphere hits the tail, but the board's rising speed slows down and gradually stops. Immediately after that, the sphere hits the tail again, increasing the board's angle further.

In the case of 10-degree or 18-degree boards, after the sphere hits, the tails become fulcrums, and the rear wheels leave the ground. In this state, the board's center of gravity is in the air, and you should be able to flip it by flicking out your front foot.
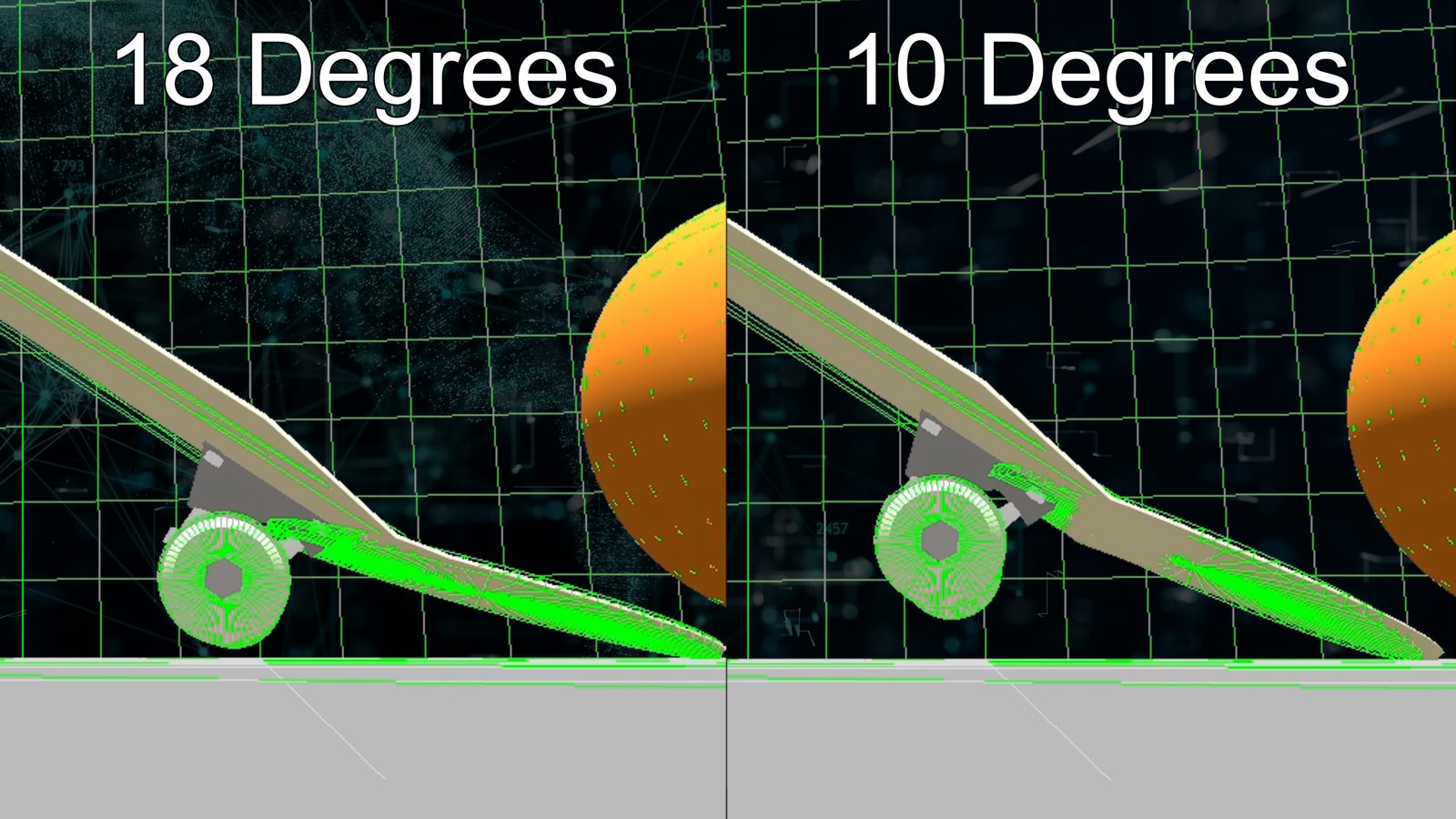
If you compare the boards before the sphere hits the tail of the 36-degree board for the second time, all three boards are almost at the same angle, but the wheels of the 36-degree board are still on the ground.
In this state, you probably won't be able to flip the board by flicking it with your front foot, indicating that the 36-degree board requires a bigger force to lift its center of gravity and allow you to control it.

Conclusion under this condition
For these reasons, the physics engine says the common belief that "you can pop the mellower tail more lightly" is correct.

Simulation: Dropping a 4.5kg sphere from 1.5m high
The 10-degree board pops the highest unlike the common saying
Generally speaking, the greater the angle of the tail, the higher the board pops, but a comparison of the three boards shows that the board with the 10-degree tail pops the highest.
This should provoke a lot of discussions but let's consider the reason for this: the tail of a 10-degree board is so close to the ground that the energy received from the sphere can hit the ground immediately, and its rebound directly pushes it back up into the air.

The 36-degree board loses its energy before hitting the ground
On the other hand, with a 36-degree board, the tail will hit the ground only after descending a long distance, at which point the board has already lost some of its energy.

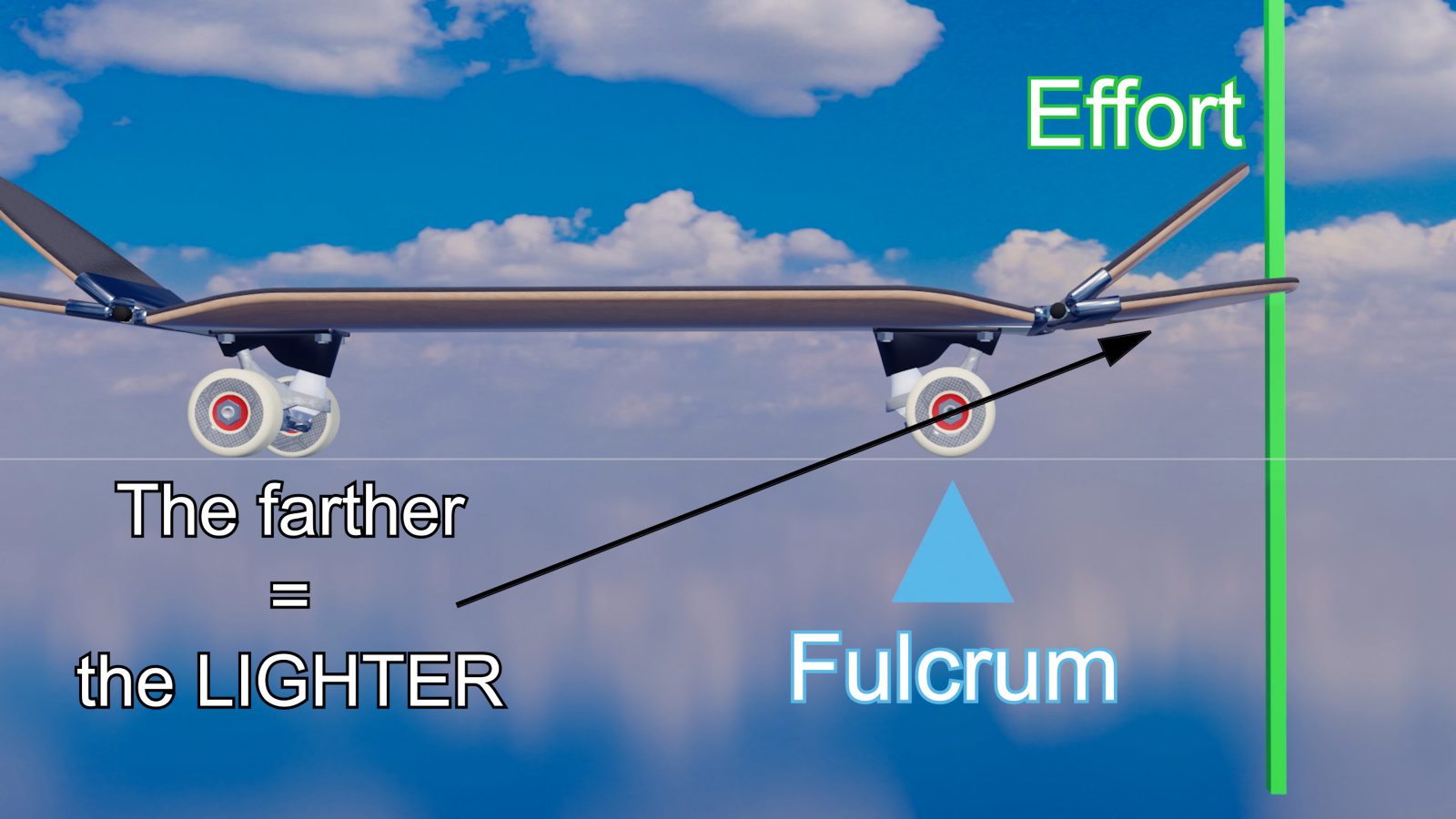
The effect of the leverage principles
If you look at the horizontal distance, you can also see that the leverage principle applies.
The looser the angle, the greater the distance from the fulcrum to the point of force; thus, it can lift the nose on the opposite side of the force more effectively.
Conclusion under this condition
Given these facts, the common saying that "the greater tail angle pops higher" is not necessarily correct from the standpoint of the board's bounce alone.

Note under this condition: Regarding the angle
However, in actual tricks, it is also essential to consider other elements, such as the role of the front foot and timing.
For example, the 36-degree board has already risen to a greater angle than the other boards when the tail hits the ground and would cause more friction with the front foot.

Note under this condition: Regarding the timing
We can also see that the board bounces up the latest because it takes the longest time until the tail hits the ground, affecting the timing.
Once again, this experiment focuses only on the board's behavior when it receives an external force on the tail.



